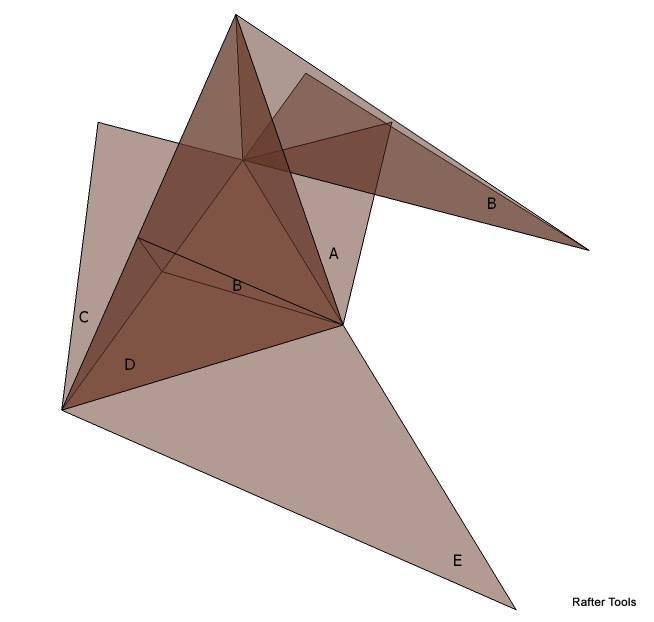
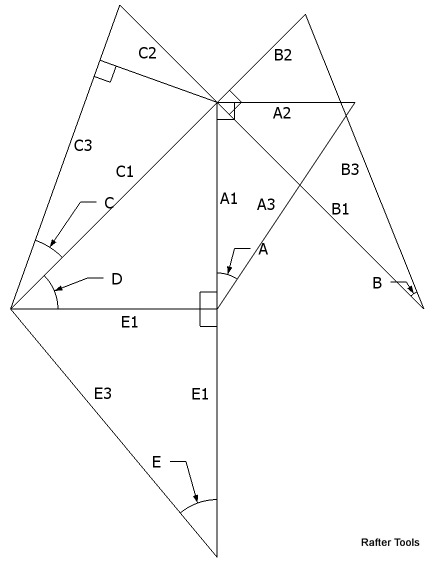
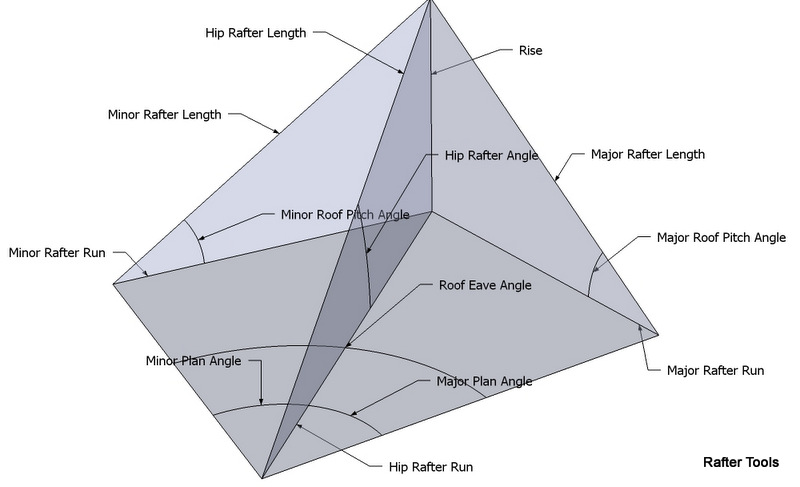
The tetrahedron calculator will calculate the angles and side lengths for a right triangle tetrahedron.
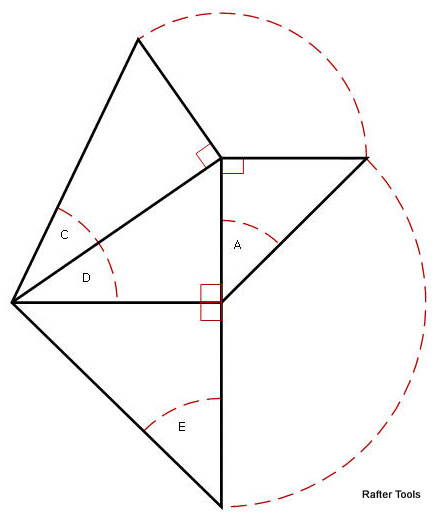
A tetrahedron is composed of four right triangles that model the angles in a Hip-Valley roof system.The tetrahedron has 6 edges and 4 faces.

Edges
• Eave Line
• Common Rafter Rise
• Common Rafter Run
• Common Rafter Length
• Hip Rafter Run
• Hip Rafter Length

Faces
• Plan Angle Face
• Common Rafter Face
• Hip Rafter Face
• Roof Sheathing Face

Tetrahedron Angle 1
Degrees input —— use any roof angle in degrees like 33.69007° or choose from the spinner below the input field to select an angle. The spinner is re-populated with new angles from the calculated tetrahedron.

Tetrahedron Angle 2
Degrees input —— use any plan angle in degrees like 45.00000° or choose from the spinner below the input field to select an angle. The spinner is re-populated with new angles from the calculated tetrahedron.

Side A1 Dimension Input Menu Mode
1. Imperial/English Inch base 12 —— default.. use American standard pitches over 12.
2. Metric 300mm base —— 300mm is 11.81102 inches, similar usage to the American framing squares printed in inches.
3. Decimal Inch base 10 —— use this option when working with tangents or using the Chappell Master Framing Square multiply the tangent of the angle by 10

The output mode selection can be completely different from the input mode

Length/Dimensions Output Menu Mode
1. Imperial/English Inch base 12 —— default.. use American standard pitches over 12.
2. Metric 300mm base —— 300mm is 11.81102 inches, similar usage to the American framing squares.
3. Decimal Inch base 10 —— use this option when working with tangents or using the Chappell Master Framing Square

Tetrahedron Calculations
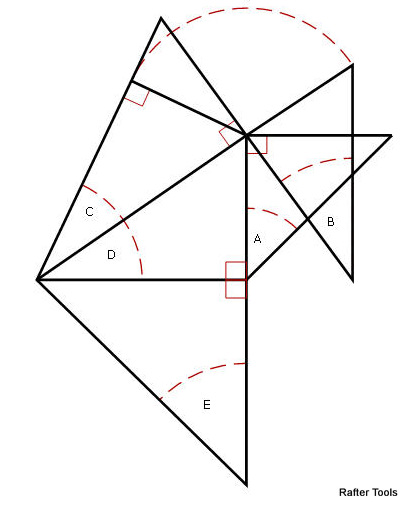
Select A,B,C,D or E from the spinner selection to calculate the rest of the tetrahedrons angles.

• Angle A can be the roof slope angle of an roof. Like 33.69007° for an 8:12 pitched roof.
• Angle B can be the hip rafter backing angle.
• Angle C can be the hip rafter slope angle.
• Angle D can be the roof plan angle.
• Angle E can be the jack rafter side cut angle.

Framing Square Usage Calculations
The calculator will print out the lengths/dimensions of the tetrahedron to be drawn with a framing square.

Tetrahedron Trigonometric Identity Formulas by Joe Bartok

• Angle C = arccos( cos( A ) ÷ cos ( B ))
• Angle C = arccos( sin ( E ) ÷ cos ( D ))
• Angle C = arcsin ( sin ( A ) × cos ( E ))
• Angle C = arcsin ( tan( D ) × tan ( B ))
• Angle C = arctan( sin ( B ) ÷ tan ( E ))
• Angle C = arctan( tan ( A ) × sin ( D ))

• Angle D = arccos( sin ( E ) ÷ cos ( C ))
• Angle D = arccos( sin ( B ) ÷ sin ( A ))
• Angle D = arcsin ( tan ( C ) ÷ tan ( A ))
• Angle D = arcsin ( cos ( B ) × cos ( E ))
• Angle D = arctan( sin ( C ) ÷ tan ( B ))
• Angle D = arctan( cos ( A ) ÷ tan ( E ))

• Angle A = arccos( cos ( C ) × cos ( B ))
• Angle A = arccos( tan ( E ) × tan ( D ))
• Angle A = arcsin ( sin ( C ) ÷ cos ( E ))
• Angle A = arcsin ( sin ( B ) ÷ cos ( D ))
• Angle A = arctan( tan ( C ) ÷ sin ( D ))
• Angle A = arctan( tan ( B ) ÷ sin ( E ))

• Angle E = arccos( sin ( D ) ÷ cos ( B ))
• Angle E = arccos( sin ( C ) ÷ sin ( A ))
• Angle E = arcsin ( cos ( D ) × cos ( C ))
• Angle E = arcsin ( tan ( B ) ÷ tan ( A ))
• Angle E = arctan( cos ( A ) ÷ tan ( D ))
• Angle E = arctan( sin ( B ) ÷ tan ( C ))

• Angle B = arccos( sin ( D ) ÷ cos ( E ))
• Angle B = arccos( cos ( A ) ÷ cos ( C ))
• Angle B = arcsin ( sin ( A ) × cos ( D ))
• Angle B = arcsin ( tan ( E ) × tan ( C ))
• Angle B = arctan( tan ( A ) × sin ( E ))
• Angle B = arctan( sin ( C ) ÷ tan ( D ))

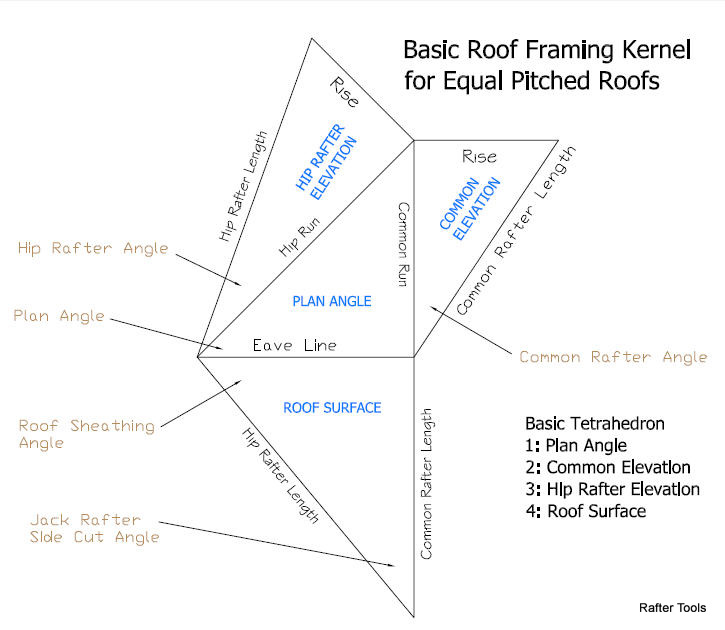
Basic Roof Framing Angles
Angle A = Roof Pitch Angle
Angle D = Plan Angle
Angle C = Hip Rafter Angle
Angle E = Jack Rafter Side Cut Angle
Angle 90-E = Roof Sheathing Angle
Angle B = Hip Rafter Backing Angle

Advanced Roof Framing Angles
Angle A = Jack Rafter Side Cut Angle
Angle D = Hip Rafter Backing Angle
Angle C = Square Tail Hip Rafter Miter Angle
Angle 90-E = Purlin Miter Angle
Angle B = Purlin Saw Blade Bevel Angle